Dijkstra's Algorithm

Dijkstra’s Algorithm

Dijkstra’s Algorithm is a shortest path algorithm that is widely used to find the minimum cost path from a source node to all other nodes in a graph. It’s especially useful in scenarios like network routing, where optimal paths between routers must be computed. During my exploration, I came across the use of Dijkstra’s Algorithm in OSPF (Open Shortest Path First) a dynamic routing protocol that uses this algorithm under the hood to determine the most efficient routes.

What I Learned About this Algorithm

• Starts with the source node and assume all other nodes are at an infinite distance.
• Visit all neighboring nodes and calculate their distance from the source using: new_cost = previous_cost + edge_cost
• If this new_cost is less than the current stored cost, update it.
• Continue this process until all nodes have been visited.

Example problem I took

graph LR
    A((A)) -->|7| B((B))
    A -->|12| C((C))
    B -->|2| C
    B -->|9| D((D))
    C -->|10| E((E))
    E -->|4| D
    E -->|5| F((F))
    D -->|1| F

For easier implementation, I calibrated the nodes for the vector: A → 0, B → 1, C → 2, D → 3, E → 4, F → 5

Program

We’ll use Rust to implement Dijkstra’s Algorithm due to its performance and expressive type system.

cargo new djax --vcs none && cd djax && code .

type Graph = Vec<Vec<(usize, usize)>>;
const INF:usize = usize::MAX;
fn main() {
    let graph = vec![
        vec![(1,7),(2,12)],
        vec![(2,2),(3,9)],
        vec![(4,10)],
        vec![(5,1)],
        vec![(3,4),(5,5)],
        vec![]
    ];
    let start = 0;
    let dist = djax(&graph, start);
    println!("{} => {:#?}", start, dist);
}


fn djax(graph:&Graph, start:usize)->Vec<usize>{
    let n = graph.len();
    let mut dist = vec![INF;n];
    let mut visited = vec![false;n];

    dist[start] = 0;

    for _ in 0..n{
        let mut mini = None;
        for i in 0..n{
            if !visited[i] && (mini.is_none() || dist[i]< dist[mini.unwrap()]){
                mini = Some(i);
            }
        }
        let u = mini.unwrap();
        visited[u] = true;

        for &(v, weight) in &graph[u]{
            let current_dist = dist[u];
            let updated_dist = current_dist+weight;

            if updated_dist< dist[v]{
                dist[v] = updated_dist;
            }
        }
    }

    dist
}

Explanation

• Node Mapping: Converted nodes A–F to 0–5 for simpler indexing.
• Graph Type Alias: Graph = Vec<Vec<(usize, usize)>>, where each entry is a (neighbor, cost) tuple.

• Initialization:

  • All distances set to INF except the start node (0).
  • All nodes are initially unvisited.

• Relaxation:

  • Select the unvisited node with the smallest distance.
  • Visit its neighbors and relax the edges if a shorter path is found.
• Repeat until all nodes are processed.

---

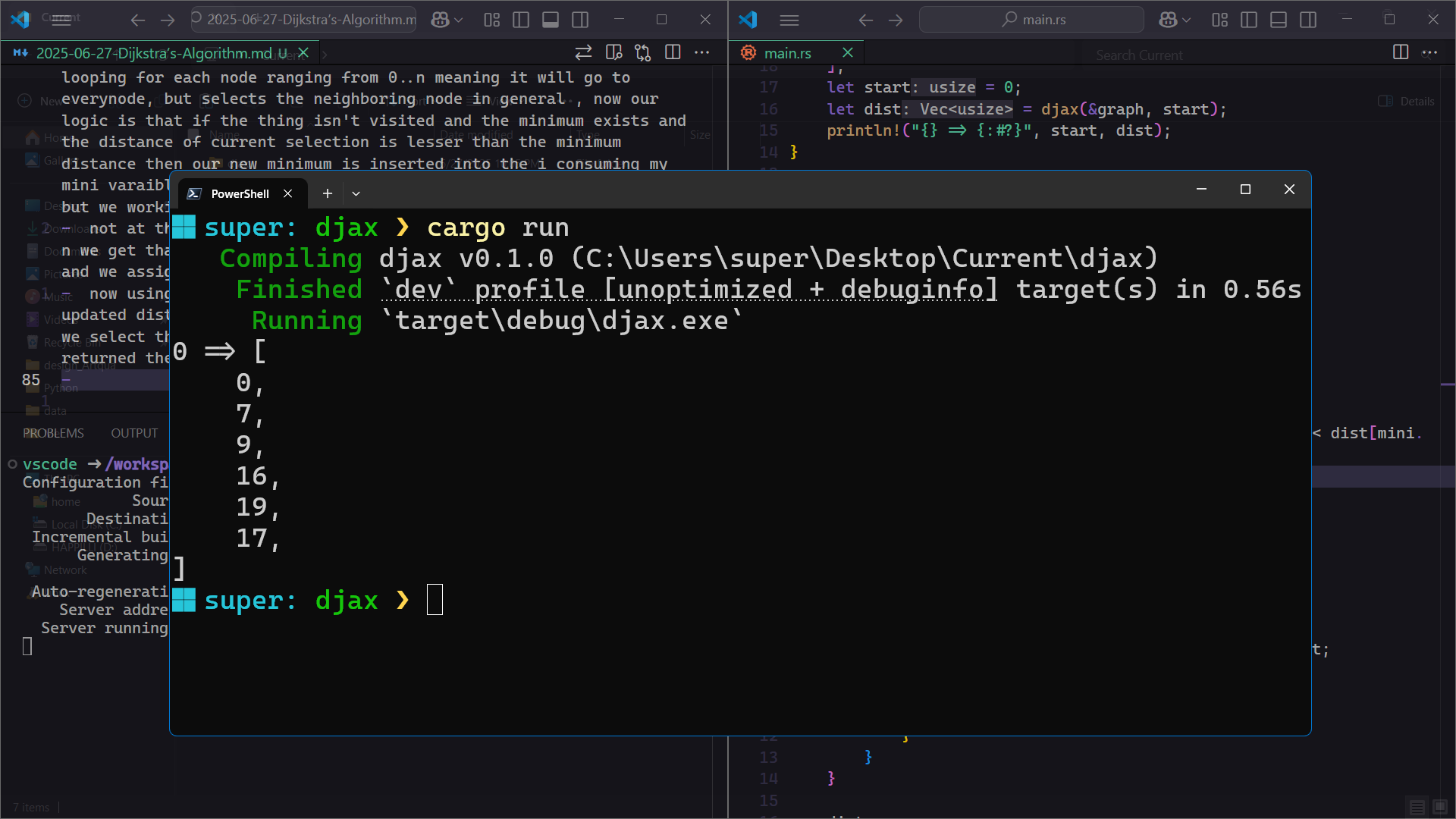
Output

Here’s the output from the terminal:

It shows the shortest distance from node A (0) to all other nodes.